PRINCÍPIO DE
ARQUIMEDES
Uma fábula da
Rússia conta a pequena estória de um camponês bem simplório que morava à beira-mar.
Todas as vezes que via passar ao largo um belo navio, corria até a praia, apanhava uma
pedra, e atirava-a na água. A pedra, naturalmente, afundava. O bom homem, olhando
admirado para imensa massa metálica do navio que flutuava magnificamente, sacudia os
punhos e bradava: "Por que ele flutua, sendo tão pesado, e a pedra não?"
De modo mais ou
menos semelhante, quando em 1787 Jonh Wilkinson lançou no rio Severn, na Inglaterra, sua
barcaça feita de ferro, as inúmeras pessoas que presenciavam o acontecimento não podiam
acreditar que aquilo flutuasse. Tinham-se reunido ali por divertimento, preparadas para
rir do desconsolo de Wilkinson quando sua chata fosse ao fundo. Mas, a embarcação
flutuou, com grande espanto e frustração dos presentes, tornando-se assim a precursora
dos modernos navios de aço.
Pode-se compreender
que o homem comum da Inglaterra, há duzentos anos atrás, não levasse a sério a
possibilidade de um navio de metal flutuar, posto que as aparências sugeriam a madeira
como único material adequado à construção de barcos.
Entretanto, não há
razão para que os princípios elementares, que explicam o fenômeno da flutuação, não
devam ser entendidos por todos nos dias de hoje.
Atualmente é banal
a construção de navios pesando muitos milhares de toneladas, que não só flutuam
perfeitamente no mar, como transportam outros milhares de toneladas de mercadorias a
bordo. Trata-se de uma banalidade porque seus projetistas e construtores conhecem
perfeitamente esta lei estabelecida por volta do ano 250 a.C. pelo sábio grego Arqimedes.
Seu enunciado nos ensina que "um corpo imerso num fluido (líquido ou gás)
perde uma quantidade de peso igual ao peso da quantidade de peso igual ao peso da
quantidade de fluido deslocado"; ou, em outras palavras, "o corpo imerso
no fluido recebe um empuxo vertical, de baixo para cima, igual ao peso do fluido
deslocado".
Certamente, muitos
dos construtores de barcos anteriores a Wilkinson conheciam também essa lei. Mesmo que
não a conhecessem, poderiam recorrer a cientistas ou técnicos para os quais as
aplicações eram claras. No entanto, havia restrições muito mais sérias, em outros
ramos da técnica. A aplicação de muitos princípios demorou mais de dois mil anos. A
inexistência de chapas de ferro ou aço, por exemplo, era a razão suficiente para tanto.
EMPUXO (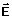 )
Um corpo mergulhado
num fluido, parcial ou totalmente, sofre pressões em toda a extensão de sua superfície
em contato com o fluido. Então, existe uma resultante das forças aplicadas pelo fluido
sobre o corpo que é chamada de empuxo. Essa força é direcionada verticalmente
para cima e opõe-se à ação da força-peso que atua no corpo.
PRINCÍPIO DE
ARQUIMEDES
"Todo corpo
imerso, total ou parcialmente, num fluido em equilíbrio, dentro de um campo
gravitacional, fica sob a ação de uma força vertical, com sentido ascendente, aplicada
pelo fluido; esta força é denominada empuxo (
)
Um corpo mergulhado
num fluido, parcial ou totalmente, sofre pressões em toda a extensão de sua superfície
em contato com o fluido. Então, existe uma resultante das forças aplicadas pelo fluido
sobre o corpo que é chamada de empuxo. Essa força é direcionada verticalmente
para cima e opõe-se à ação da força-peso que atua no corpo.
PRINCÍPIO DE
ARQUIMEDES
"Todo corpo
imerso, total ou parcialmente, num fluido em equilíbrio, dentro de um campo
gravitacional, fica sob a ação de uma força vertical, com sentido ascendente, aplicada
pelo fluido; esta força é denominada empuxo (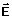 ), cuja intensidade é igual à do peso do
fluido deslocado pelo corpo."
E = Pfd =
mfd . g = df . Vfd . g
E = df . Vfd
. g
onde df =
densidade do fluido e Vfd = volume do fluido deslocado.
), cuja intensidade é igual à do peso do
fluido deslocado pelo corpo."
E = Pfd =
mfd . g = df . Vfd . g
E = df . Vfd
. g
onde df =
densidade do fluido e Vfd = volume do fluido deslocado.
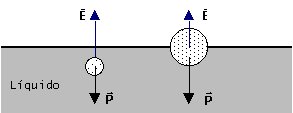 Obs.: O valor do
empuxo não depende da densidade do corpo imerso no fluido; a densidade do corpo (dc)
é importante para se saber se o corpo afunda ou não no fluido.
Obs.: O valor do
empuxo não depende da densidade do corpo imerso no fluido; a densidade do corpo (dc)
é importante para se saber se o corpo afunda ou não no fluido.
| dc < df => O corpo pode
flutuar na superfície do fluido (no caso de líquido). |
| dc = df => O corpo fica em
equilíbrio no interior do fluido (com o corpo total mente imerso). |
| dc > df => O corpo
afunda no fluido. |
O empuxo é uma
força que resulta da diferença de pressão existente entre pontos de diferentes níveis
no interior de um fluido.
No caso particular
de um corpo (como mostra a figura), de secção transversal de área (A) constante, como
um cilindro por exemplo é determinado por:
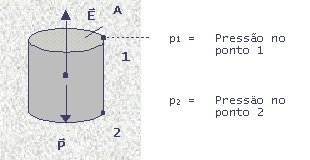 E = (p2 – p1) . A
E =
E = (p2 – p1) . A
E =  p . A
ou pois, pelo
Teorema de Stevin,
p . A
ou pois, pelo
Teorema de Stevin,
 p = df
. g .
p = df
. g .  h e E = df . g .
h e E = df . g .  h. A ou,
como Vfd =
h. A ou,
como Vfd =
 h
. A, E = df . Vfd . g
h
. A, E = df . Vfd . g
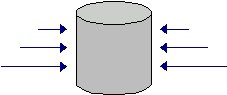
Obs.: As forças
laterais-horizontais diametralmente opostas, anulam-se duas a duas.
Portanto, a resultante horizontal
das forças exercidas pelo fluido é nula.
Unidades principais:
|
E |
d |
V |
g |
p |
A |
| No SI |
N |
Kg/m3 |
m3 |
m/s2 |
N/m2 |
m2 |
| No CGS |
dyn |
g/cm3 |
cm3 |
cm/s2 |
dyn/cm2 |
cm2 |
| No MK*S |
Kgf |
utm/m3 |
m3 |
m/s2 |
kgf/m2 |
m2 |
PESO APARENTE
Quando um corpo é
totalmente imerso num fluido de densidade menor do que a sua, o peso tem intensidade maior
do que a do empuxo. A resultante dessas forças é denominada peso aparente (Pap):
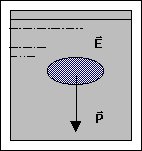
dc > df
=> P > E
e Pap =
P – E
O peso aparente
também pode ser medido de um dinamômetro.
CORPOS EM
EQUILÍBRIO
Um corpo na
superfície de um líquido, quando abandonado, se a densidade do corpo for menor do que a
do líquido. Na posição de equilíbrio (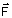 r
=
r
= 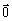 ), o empuxo e o peso devem ter a mesma
intensidade, em valor absoluto:
), o empuxo e o peso devem ter a mesma
intensidade, em valor absoluto:
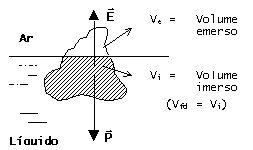 E = P ou
df . Vfd . g = dc . Vc . g
E = P ou
df . Vfd . g = dc . Vc . g
Logo: df .
Vi = dc . Vc
Volume
do corpo (Vc):
Vc
= Ve + Vi
Obs.: Lembre-se de que dc
. Vc = mc; portanto: df . Vi = mc
Atenção: Neste caso, o empuxo
exercido pelo ar é desprezível.
Caso o corpo esteja em
equilíbrio entre vários líquidos, tem-se:
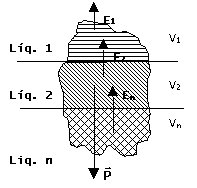
E1 + E2 + En
= P
ou (:g)
d1 . V1 + d2 . V2
+ dn . Vn = dc . Vc



 Obs.: O valor do
empuxo não depende da densidade do corpo imerso no fluido; a densidade do corpo (dc)
é importante para se saber se o corpo afunda ou não no fluido.
Obs.: O valor do
empuxo não depende da densidade do corpo imerso no fluido; a densidade do corpo (dc)
é importante para se saber se o corpo afunda ou não no fluido.
 E = (p2 – p1) . A
E =
E = (p2 – p1) . A
E = 

![]() r
=
r
= ![]() ), o empuxo e o peso devem ter a mesma
intensidade, em valor absoluto:
), o empuxo e o peso devem ter a mesma
intensidade, em valor absoluto: E = P ou
df . Vfd . g = dc . Vc . g
E = P ou
df . Vfd . g = dc . Vc . g
![]()